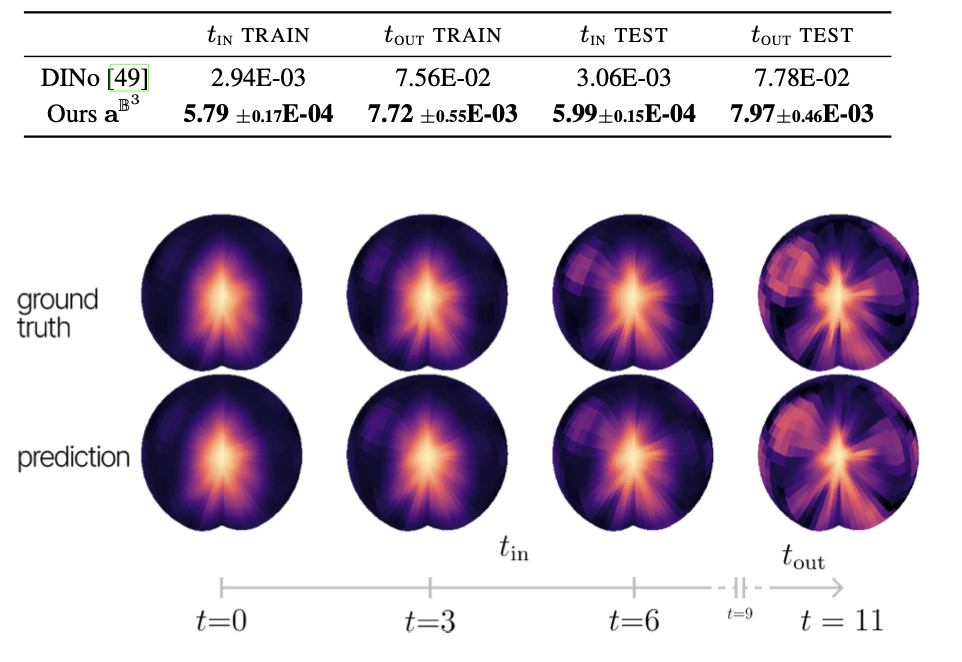
Space-Time Continuous PDE Forecasting using Equivariant Neural Fields
NeurIPS, 2024
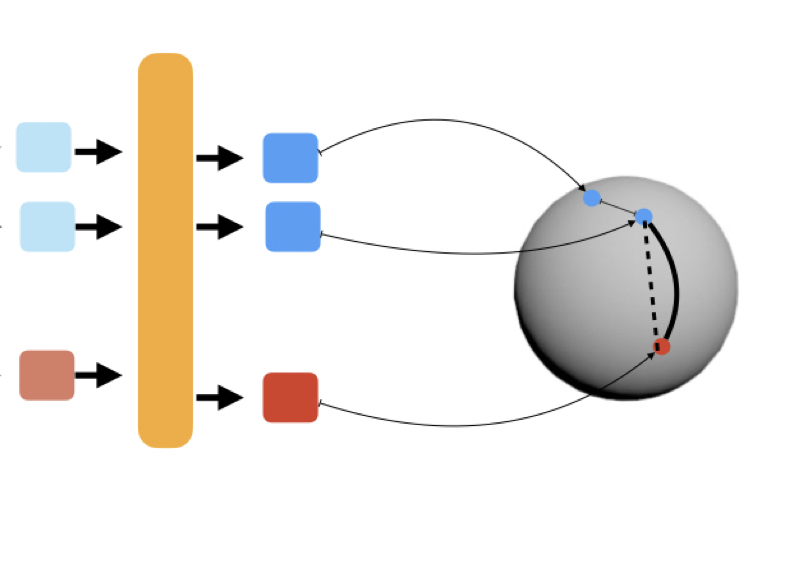
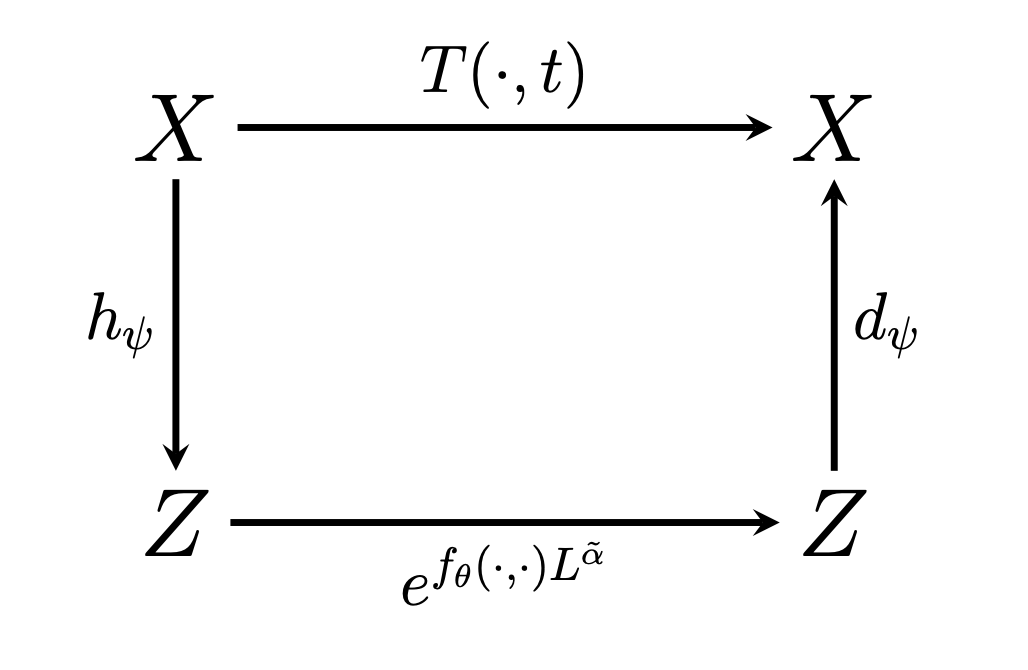
Recently, Conditional Neural Fields (NeFs) have emerged as a powerful modelling paradigm for PDEs, by learning solutions as flows in the latent space of the Conditional NeF. Although benefiting from favourable properties of NeFs such as grid-agnosticity and space-time-continuous dynamics modelling, this approach limits the ability to impose known constraints of the PDE on the solutions – e.g. symmetries or boundary conditions – in favour of modelling flexibility. Instead, we propose a space-time continuous NeF-based solving framework that - by preserving geometric information in the latent space - respects known symmetries of the PDE. We show that modelling solutions as flows of pointclouds over the group of interest G improves generalization and data-efficiency. We validated that our framework readily generalizes to unseen spatial and temporal locations, as well as geometric transformations of the initial conditions - where other NeF-based PDE forecasting methods fail - and improve over baselines in a number of challenging geometries.